Malcolm Gladwell v. Chess

In Season 4, Episode 3 of his podcast Revisionist History, Malcolm Gladwell argues against the use of the LSAT in law school admissions. A full transcript of the episode can be read here.

In this post, we’ll examine the quantiative evidence Gladwell cites – competitive chess ratings – in support of his argument that “fast” and “slow” thinking skills are unique and uncorrelated cognitive abilities, and through some simple exploratory analysis come to the opposite conclusion of Gladwell.

Motivation

In the podcast episode, Gladwell makes the following arguments:

1. There are two types of thinking – “fast” and “slow.”

“Fast thinking” is the ability to think quickly and make snap judgements. Gladwell refers to people who excel at this as “hares.”

“Slow thinking” is the ability to contemplate a problem over a long period of time. He refers to people who excel at this as “tortoises.”

2. “Fast” and “slow” thinking are distinct cognitive abilities that are not well-correlated, i.e. it is not sufficient to simply test for one as a proxy of the other.

As evidence, Gladwell makes an analogy to competitive chess rankings, pointing out that the world’s top-20 players in blitz chess (“fast thinking”) have different ratings than they have in classical chess (“slow thinking”).

3. The LSAT exclusively tests “fast thinking” skills.

The LSAT a timed test. As the The Princeton Review notes, “the average test taker should not be able to comfortably complete all the questions in the time allotted.”

This unfairly disadvantages “slow” thinkers, even though “slow” thinking is a more useful skill for being a lawyer.

4. Thus, the LSAT is a misguided test for law school admissions, as it arbitrarily evaluates the wrong type of thinking.

As Gladwell explains:

“The LSAT is Exhibit A. It’s the single most important thing that determines where you go to law school. Nothing else comes close. And what is it? It’s around 125 questions, divided among five sections…

And how long do you get to spend on each of those five sections? 35 minutes…When we decide who is smart enough to be a lawyer, we use a stopwatch…

My mother is a little bit of a tortoise. She will not be rushed under any circumstances. She does not make mistakes…She’d have a problem with the LSAT. She would say, “Why are you rushing me?” and she wouldn’t finish…

The profession is putting up a barrier to my mom.”

The Question

In this post, I won’t be discussing Gladwell’s argument about the LSAT directly.

Rather, I’d like to dissect his cherry-picked anecdote about chess ratings (on which he spends roughly half the podcast).

In Gladwell’s words:

“Everything about blitz and classical is the same - same pieces, same board, same players, same choreographed openings, but the time limits are different.

And what happens when you tinker with the time limit? You get a completely different set of results.

At classical chess, Magnus Carlsen is number one. He’s also number one at blitz because he’s a genius. Hikaru, right now, is 11th in the classical rankings but, at blitz, he’s number two in the world.

Why? Because he’s really, really good at the rapid pattern recognition that’s necessary for blitz and he’s not quite as good at the complex calculation that’s necessary for classical.”

Culminating in Gladwell’s big insight for the episode…

“[T]he order in which people finish in any cognitive task is an arbitrary function of how much time is given to complete that task. You can make it fast or you can make it slow.

The chess world has chosen to reward the tortoise, the LSAT has chosen to reward the hare.”

Can we draw such broad conclusions from a sample of $n = 2$ chess players?

Obviously, no.

But I was curious – what conclusions can we draw about “fast” and “slow” thinking from the entire population of competitive chess players?

Do chess ratings actually indicate that “fast” and “slow” thinking are distinct skillsets, or does the data tell a different story?

The Data

To start, I downloaded the entire FIDE rating list for April, 2021 here from Kaggle.

The dataset had a total of 433,388 unique players with a FIDE rating in at least one of chess’s three main events: classical, blitz, and rapid.

The number of players in each event, as well as the number of overlaps, is as follows:

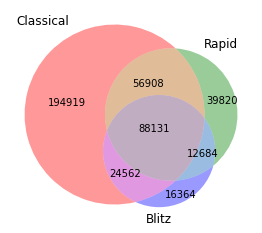
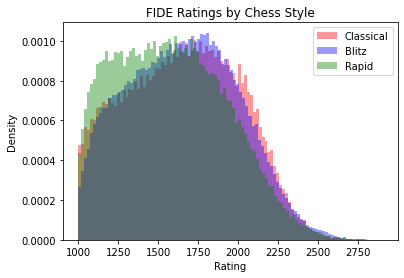
As the below histograms show, the ratings within each event have similar distributions. Note that the higher the rating, the better the player, so there’s a noticeable right tail of top players (e.g. Magnus Carlsen).

Analysis

I’ll recopy Gladwell’s thesis below for reference:

“[T]he order in which people finish in any cognitive task is an arbitrary function of how much time is given to complete that task.”

Let’s assume for the sake of argument that everything else he says is true – namely, that chess is an accurate model of human cognitive abilities, and that blitz chess measures “fast thinking” while classical chess measures “slow thinking.”

If Gladwell’s claims about the independence of “slow” and “fast thinking” are true, then we would expect to see minimal correlation between an individual’s classical and blitz chess ratings.

On the other hand, if “fast” and “slow” thinking are simply alternative manifestations of the same underlying general cognitive ability, then we’d expect to see a strong correlation between classical and blitz ratings.

To assess this, we can simply measure the Pearson correlation between every player’s classical and blitz rating.

Below is that graph for the top-20 players in classical and blitz chess (each dot is an individual chess player):

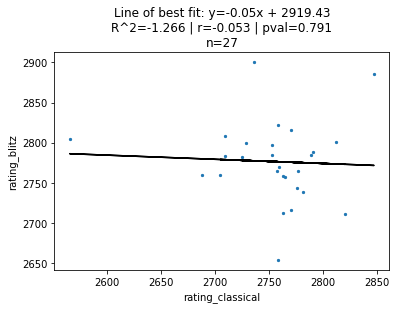
Here, $n$ is the total number of players included in the analysis, $R^2$ is the coeffecient of determination, $r$ is the Pearson correlation, and $pval$ is the p-value of the Pearson coeffecient. Each data point is an individual chess player – the top-right-most one is Magnus Carlsen, widely recognized as the greatest chess player of all time.

I’ve also plotted the line of best fit, although the relationship between the two ratings may not necessarily be linear. Also, since the sets of players compared are not the same (i.e. the top-20 blitz players are not the same as the top-20 classical players), I simply took the union of both lists. This is why $n$ is not exactly 20 in the above plot of top-20 players.

Ignoring the super high p-value of $p = 0.791$, it seems that Gladwell might be right – there appears to be no correlation ($r = -0.053$) in how the top-20 ranked classical and blitz players are ordered.

But Gladwell was using chess as an analogy for the LSAT, and the LSAT doesn’t just test the top-20 lawyers in the country – rather, it tests everyone who’s applying to law school.

And we have a ton of data at our fingertips. Instead of making up an arbitrary cutoff without statistical significance, let’s see what happens when we zoom out and consider more of the dataset.

Below is the same plot, but for the top-1000 players in classical and blitz chess.

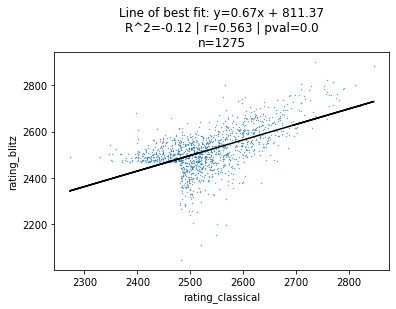
Immediately, our correlation jumps from $r = -0.053$ to $r = 0.563$.

Still, we’re only looking at a fraction of our dataset.

Let’s zoom out even more and consider all 112,963 players who have either a classical or blitz rating in the FIDE database.

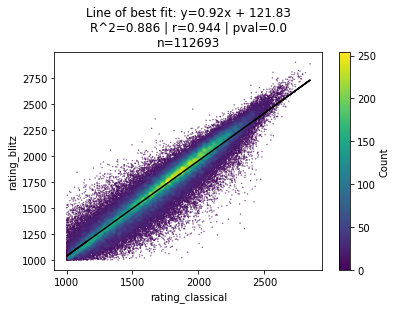
Now we’re seeing the whole picture.

When looking at the entire dataset, we see a very strong correlation ($r = 0.944$) between an individual’s classical and blitz chess ratings.

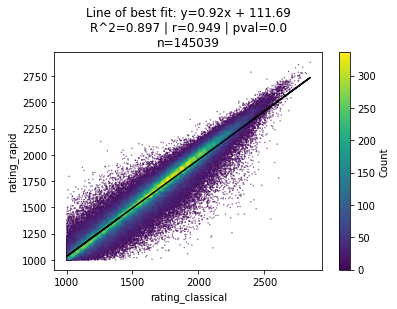
We see similarly strong correlations whether we compare classical v. rapid ratings…

…or blitz v. rapid ratings…

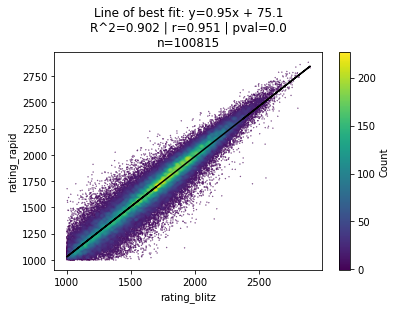
If, as Gladwell argues, chess is a reliable analogy for the LSAT (and human cognition in general), then it seems like we’ve come to an entirely different conclusion.

At the population-level, the data strongly disagrees with Gladwell’s assertion that:

"[T]he order in which people finish in any cognitive task is an arbitrary function of how much time is given to complete that task."

At least in the world of chess, “fast” and “slow” thinking seem to be derived from the same underlying cognitive ability – good chess players perform well regardless of the specific format or “speed” of the game.

Thus, testing for one “speed” of thinking gives you very reliable information of a person’s ability in the other “speed.”

This seems intuitive – smart people tend to do smart things. The valedictorian of your high school got straight A’s in every subject, whether it was history or pre-calculus or english.

Pragmatically speaking, this suggests that if you have finite resources then you should test whichever “speed” is cheaper to evaluate. I suspect that “fast” thinking is much cheaper to test since, by definition, it requires less time to measure. Hence, the LSAT.

Analysis, pt. 2

In addition to quantifying the variation of ratings across players, we can measure the variation between an individual’s “slow” and “fast” thinking abilities.

We’ve just established that smart people tend to do smart things regardless of the “speed” of the task.

Now, we’d like to know how varied a smart person’s performance is within those tasks.

Let’s say a player $C$ has a rating of $C_A$ in classical chess and $C_B$ in blitz chess. Then the value $C_A - C_B$ is the difference between their “fast” and “slow” thinking abilities.

A histogram of the values of $|C_A - C_B|$ for all 112,963 players who competed in both classical and blitz chess is below.

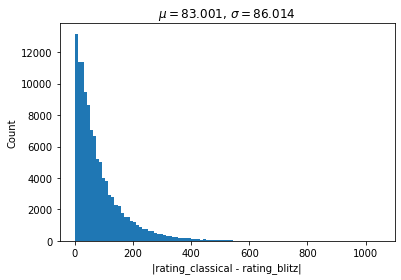
The mean absolute difference in ratings is $\mu = 83$, with a median absolute difference of $56$ and a standard deviation of $\sigma = 86$.

Here is the CDF of the distribution of $|C_A - C_B|$, showing that roughly 60% of players have an absolute difference in their classical v. blitz ratings of less than 100.

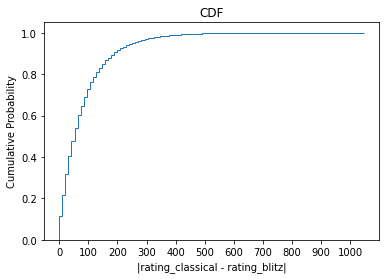
How do we interpret this?

In chess, having a +100 point advantage over your opponent corresponds to a +15% increased probability of winning the match (i.e. you go from a 50% chance of winning to 65%).

A change of +/- 100 rating points would definitely shake up the chess rankings. But grandmasters would still be grandmasters, bad players would still be bad, and so on.

This seems to agree with our previous macro-level analysis, as these individual-level variations in skill wouldn’t make a huge difference in our assessment of player skill levels at the population-level.

So, to give Gladwell credit, there is measurable variation in an individual’s “fast” and “slow” thinking abilities.

Conclusion

So where does that leave us?

At an individual level, there is variation in “fast” and “slow” thinking abilities, as Gladwell notes.

But that’s not very controversial – everyone knows that they’re better at some things than others.

What is controversial – and interesting enough to build a 30-minute podcast around – is Gladwell’s broader assertion that:

"[T]he order in which people finish in any cognitive task is an arbitrary function of how much time is given to complete that task."

But, as we’ve seen with chess, this broader claim about population-level orderings does not hold true.

Thus, Gladwell’s claim is either so specific it is obvious, or so broad it is empirically false.

This nuance between individual-level and population-level statistics is especially relevant when making an analogy to a test like the LSAT, which is administered at the population-level and whose explicit purpose is to create a standardized testing environment for students.

At least in the chess world, “fast” and “slow” thinking appear to be two sides of the same coin.

And so, if chess ratings are a reliable analogy for law as Gladwell makes them to be, then assessments of “fast thinking” necessarily give us a strong sense of a person’s relative abilities in “slow thinking.” Thus, it makes pragmatic sense to measure the easier-to-measure of the two and call it a day.

In this context, Steven Pinker’s 2009 critique of Gladwell rings especially true:

“Another example of an inherent trade-off in decision-making is the one that pits the accuracy of predictive information against the cost and complexity of acquiring it.

Gladwell notes that I.Q. scores, teaching certificates and performance in college athletics are imperfect predictors of professional success. This sets up a “we” who is “used to dealing with prediction problems by going back and looking for better predictors.”

Instead, Gladwell argues, “teaching should be open to anyone with a pulse and a college degree — and teachers should be judged after they have started their jobs, not before.”

But this “solution” misses the whole point of assessment, which is not clairvoyance but cost-effectiveness.

To hire teachers indiscriminately and judge them on the job is an example of “going back and looking for better predictors”: the first year of a career is being used to predict the remainder. It’s simply the predictor that’s most expensive (in dollars and poorly taught students) along the accuracy-­cost trade-off.”